AutoML 中的预测方法概述
本文重点介绍 AutoML 用于准备时序数据和生成预测模型的方法。 有关在 AutoML 中训练预测模型的说明和示例，请参阅为时序预测设置 AutoML 一文。
AutoML 使用几种方法来预测时序值。 这些方法大致可以分为两类：
- 使用目标数量的历史值对未来进行预测的时序模型。
- 使用预测变量预测目标值的回归或解释模型。
例如，来看一个问题，我们要预测一家杂货店对特定品牌橙汁的每日需求。 用 $y_t$ 表示第 $t$ 天对该品牌的需求。 一个时序模型使用历史需求的某些函数预测 $t+1$ 的需求，
$y_{t+1} = f(y_t, y_{t-1}, \ldots, y_{t-s})$.
函数 $f$ 通常具有我们使用过去观测到的需求进行优化的参数。 $f$ 用于进行预测的历史量 $s$ 也可以被视为模型的一个参数。
橙汁需求示例中的时序模型可能不够准确，因为它只使用了过去的需求信息。 还有许多其他因素可能会影响未来需求，如价格、星期几以及是否是节假日。 来看看使用以下预测变量的一个回归模型，
$y = g(\text{price}, \text{day of week}, \text{holiday})$.
同样，$g$ 通常有一组参数（包括那些管理正则化的参数），AutoML 利用过去的需求值和预测变量的值进行调整。 我们从表达式中省略 $t$，以强调回归模型使用同期定义的变量之间的相关模式来进行预测。 也就是说，要从 $g$ 预测 $y_{t+1}$，我们必须知道 $t+1$ 是星期几，是否是节假日，以及 $t+1$ 当天的橙汁价格。 前两项信息始终可以通过查阅日历轻松找到。 零售价格通常是提前设定的，因此橙汁的价格很可能提前一天就知道了。 但是，未来 10 天的价格可能还不得而知！ 请务必了解，这种回归的效用受限于我们需要预测多远的未来（也称为“预测范围”），以及我们对预测变量的未来值的了解程度。
重要
AutoML 的预测回归模型假设用户提供的所有特征在未来都是已知的，至少在预测范围内是已知的。
此外，还可以扩充 AutoML 的预测回归模型，以使用目标和预测变量的历史值。 由此得到一个具有时序模型和纯回归模型特征的混合模型。 历史数量是回归中的附加预测变量，我们将它们称为“滞后数量”。 滞后的顺序是指该值可以追溯到多远以前。 例如，在我们的橙汁需求示例中，目标的两个滞后顺序的当前值是两天前观测到的橙汁需求。
时序模型与回归模型之间的另一个显著区别在于它们生成预测的方式。 时序模型一般由递归关系定义，并一次生成一个预测。 为了预测未来的多个时段，它们会循环访问预测范围，将以前的预测反馈到模型中，以便在需要时生成下一个提前一个时段的预测。 相比之下，回归模型是所谓的直接预测器，可以一次性生成范围内的所有预测。 直接预测器可能比递归预测器更好，因为递归模型在将以前的预测反馈到模型时，会将预测误差混淆在一起。 当包含滞后特征时，AutoML 会对训练数据进行一些重要的修改，让回归模型可以充当直接预测器。 有关更多详细信息，请参阅滞后特征文章。
AutoML 中的预测模型
下表列出了 AutoML 中实现的预测模型以及它们所属的类别：
| 时序模型 | 回归模型 |
|---|---|
| Naive、Seasonal Naive、Average、Seasonal Average、ARIMA(X)、指数平滑法 | Linear SGD、LARS LASSO、弹性网络、Prophet、K 最近的邻域、决策树、随机林、极端随机树、梯度提升树、LightGBM、XGBoost、时间卷积网络 |
每个类别的模型大致按它们能够纳入的模式的复杂性（也称为模型容量）排列。 Naive 模型仅预测最后一个观测值，它的容量较低，而时间卷积网络 (TCN) 是一个可能具有数百万个可优化参数的深度神经网络，具有较高的容量。
重要的是，AutoML 还包括集成模型，这些模型创建性能最佳的模型的加权组合，进一步提高准确性。 对于预测，我们使用软投票集成，通过 Caruana 集成选择算法找到组成和权重。
注意
对于预测模型集成，有两个重要的注意事项：
- 目前，TCN 不能包含在集成中。
- 默认情况下，AutoML 禁用另一个集成方法，即堆栈集成，它包含在 AutoML 中的默认回归和分类任务中。 堆栈集成对最佳模型预测进行元模型拟合，以找到集合权重。 我们在内部基准测试中发现，这种策略更倾向于过度拟合时序数据。 这可能会导致泛化不佳，因此默认情况下堆栈集成处于禁用状态。 但是，如果需要，可以在 AutoML 配置中启用它。
AutoML 如何使用数据
AutoML 接受表格形式的“宽”格式时序数据，也就是说，每个变量必须有自己的对应列。 AutoML 要求其中一列作为预测问题的时间轴。 此列必须可分析为日期/时间类型。 最简单的时序数据集由时间列和数字目标列组成。 目标是打算预测未来的变量。 下面是此简单情况下的格式示例:
| timestamp | quantity |
|---|---|
| 2012-01-01 | 100 |
| 2012-01-02 | 97 |
| 2012-01-03 | 106 |
| ... | ... |
| 2013-12-31 | 347 |
在更复杂的情况下，数据可能包含与时间索引对齐的其他列。
| timestamp | SKU | price | 已播发 | quantity |
|---|---|---|---|---|
| 2012-01-01 | JUICE1 | 3.5 | 0 | 100 |
| 2012-01-01 | BREAD3 | 5.76 | 0 | 47 |
| 2012-01-02 | JUICE1 | 3.5 | 0 | 97 |
| 2012-01-02 | BREAD3 | 5.5 | 1 | 68 |
| ... | ... | ... | ... | ... |
| 2013-12-31 | JUICE1 | 3.75 | 0 | 347 |
| 2013-12-31 | BREAD3 | 5.7 | 0 | 94 |
在此示例中，有一个 SKU、一个零售价格和一个标志，指示除了时间戳和目标数量外，是否播发了某个项。 此数据集中显然有两个序列 - 一个用于 JUICE1 SKU，一个用于 BREAD3 SKU；SKU 列是一个时序 ID 列，因为按其分组会得到两个组，每个组包含一个序列。 在扫描模型之前，AutoML 会对输入配置和数据进行基本验证，并添加工程化特征。
数据长度要求
要训练预测模型，必须具有足够的历史数据量。 此阈值数量因训练配置而异。 如果已提供验证数据，则每个时序所需的训练观测的最小数由以下内容提供，
$T_{\text{user validation}} = H + \text{max}(l_{\text{max}}, s_{\text{window}}) + 1$,
其中，$H$ 是预测范围，$l_{\text{max}}$ 是最大滞后顺序，$s_{\text{window}}$ 是滚动聚合功能的窗口大小。 如果使用交叉验证，则最小观测数为，
$T_{\text{CV}} = 2H + (n_{\text{CV}} - 1) n_{\text{step}} + \text{max}(l_{\text{max}}, s_{\text{window}}) + 1$,
其中，$n_{\text{CV}}$ 是交叉验证折叠数，$n_{\text{step}}$ 是 CV 步长大小或 CV 折之间的偏移量。 这些公式背后的基本逻辑是，对于每个时序，应始终至少有一个训练观测范围，包括滞后和交叉验证拆分的一些填充。 有关预测交叉验证的更多详细信息，请参阅 预测模型选择。
缺少数据处理
AutoML 的时序模型要求及时定期间隔观测。 这里的定期间隔包括每月或每年观测等情况，其中两次观测之间的天数可能会有所不同。 在建模之前，AutoML 必须确保序列的值没有缺失 ，且 观测定期进行。 因此，存在两种数据缺失的情况：
- 表格数据中的某个单元格缺少一个值
- 与给定时序频率的预期观测对应的一个行缺失
在第一种情况下，AutoML 使用常见的可配置技术来插补缺失的值。
下表显示了缺失的预期行的示例：
| timestamp | quantity |
|---|---|
| 2012-01-01 | 100 |
| 2012-01-03 | 106 |
| 2012-01-04 | 103 |
| ... | ... |
| 2013-12-31 | 347 |
此序列表面上有每日频率，但没有 2012 年 1 月 2 日的观测结果。 在这种情况下，AutoML 将为 2012 年 1 月 2 日新增行以尝试填充数据。 然后，quantity 列的新值以及数据中的任何其他列将像其他缺失值一样进行插补。 显然，AutoML 必须知道序列频率才能填补这样的观测空白。 AutoML 会自动检测此频率，或者，用户也可以在配置中提供此频率。
可以在输入中 配置 用于填充缺失值的插补方法。 下表列出了默认的方法：
| 列类型 | 默认插补方法 |
|---|---|
| 目标 | 前向填充（最后一个观测接后） |
| 数值特征 | 中值 |
分类特征的缺失值在数值编码过程中进行处理，方法是加上与缺失值对应的附加类别。 在这种情况下，插补是隐式的。
自动化特征工程
AutoML 一般会向用户数据新增列，从而提高建模准确度。 工程化特征可以包括以下内容：
| 功能组 | 默认/可选 |
|---|---|
| 派生自时间索引(例如星期几)的 日历特征 | 默认 |
| 派生自时序 ID 的分类特征 | 默认 |
| 将分类类型编码为数值类型 | 默认 |
| 与给定的国家或地区关联的节假日的指示器特征 | 可选 |
| 目标数量滞后 | 可选 |
| 特征列滞后 | 可选 |
| 目标数量的滚动窗口聚合（例如滚动平均） | 可选 |
| 季节性分解 (STL) | 可选 |
可以通过 ForecastingJob 类或 Azure 机器学习工作室 Web 界面 从 AutoML SDK 配置特征化。
非稳定时序检测和处理
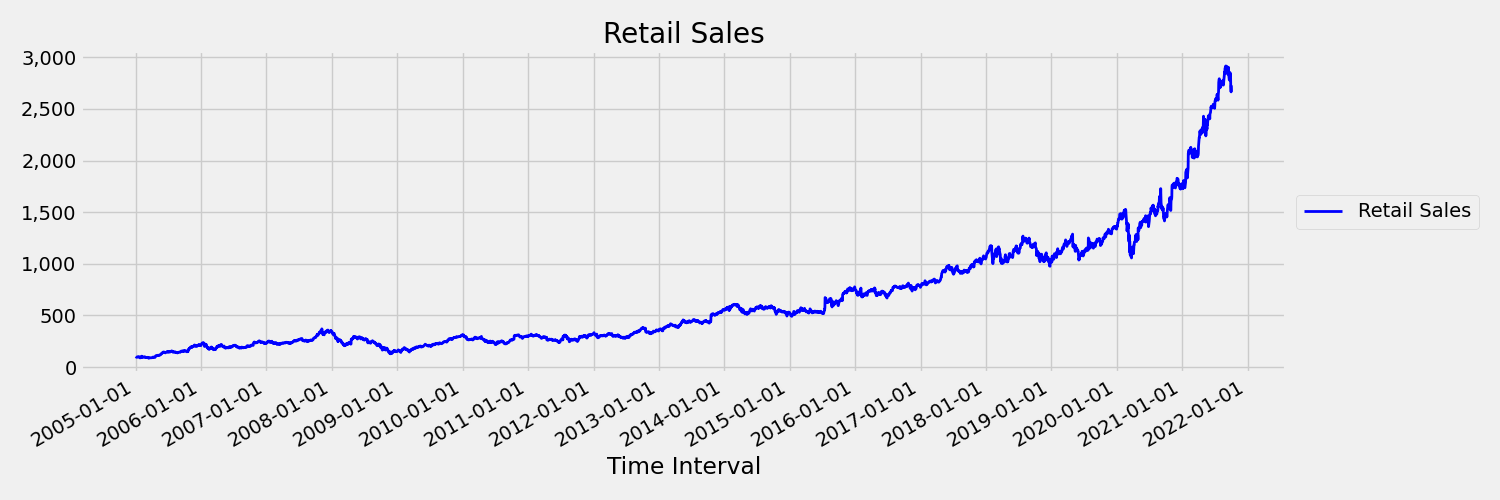
平均值和方差随时间变化的时序称为 非静态。 例如，表现出随机趋势的时序本质上是非稳定的。 为了可视化这一点，下图绘制了通常呈上升趋势的序列。 现在，计算并比较序列的前半部分和后半部分的平均值。 他们是一样的吗？ 这里，在图中，前半部分的序列平均值明显小于后半部分。 序列的平均值取决于所观察的时间间隔，这一事实是随时间变化的矩的一个示例。 在这里，序列的平均值是第一个矩。
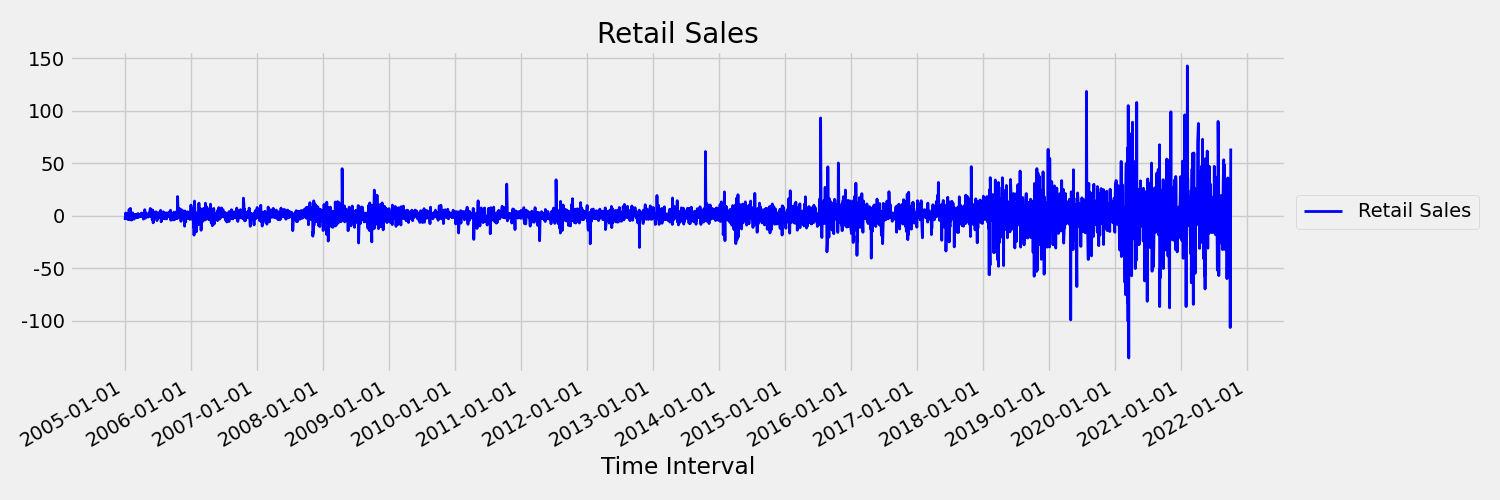
接下来，让我们看看下图，该图以一阶差分绘制了原始序列，$\Delta y_{t} = y_t - y_{t-1}$。 序列的平均值在时间范围内大致恒定，而方差似乎会有所不同。 因此，这是一阶静态时序的示例。
AutoML 回归模型本身无法处理随机趋势，或与非静态时序相关的其他已知问题。 因此，如果存在这种趋势，样本外预测准确度会较差。
AutoML 会自动分析时序数据集以确定静止性。 检测到非静态时序时，AutoML 会自动应用差分转换以减轻非静态行为的影响。
模型扫描
在通过缺失数据处理和特征工程对数据进行准备后，AutoML 使用模型建议服务扫描一组模型和超参数。 模型基于验证或交叉验证指标进行排名，然后可以选择在集成模型中使用排名靠前的模型。 可以检查、下载或部署最佳模型或任何经过训练的模型，从而根据需要生成预测。 有关更多详细信息，请参阅模型扫描和选择一文。
模型分组
当数据集包含多个时序时，如给定数据示例中所示，可以通过多种方式为该数据建模。 例如，我们可以简单地按时序 ID 列分组，并为每个序列训练独立的模型。 一个更普遍的方法是将数据划分为若干组，每个组可能包含多个可能相关的序列，并为每个组训练一个模型。 默认情况下，AutoML 预测使用混合方法进行模型分组。 时序模型，加上 ARIMAX 和 Prophet，将一个序列分配给一个组，而其他回归模型将所有序列分配给单个组。 下表总结了两个类别的模型分组：一对一和多对一：
| 每个序列位于自己的组中 (1:1) | 所有序列位于单个组中 (N:1) |
|---|---|
| Naive、Seasonal Naive、Average、Seasonal Average、指数平滑、ARIMA、ARIMAX、Prophet | Linear SGD, LARS LASSO, 弹性网络, K 最近邻算法, 决策树, 随机森林, 极度随机树, 梯度提升树, LightGBM, XGBoost, TCNForecaster |
通过 AutoML 的多模型解决方案，可以实现更普遍的模型分组；请参阅我们的多模型 - 自动化 ML 笔记本。